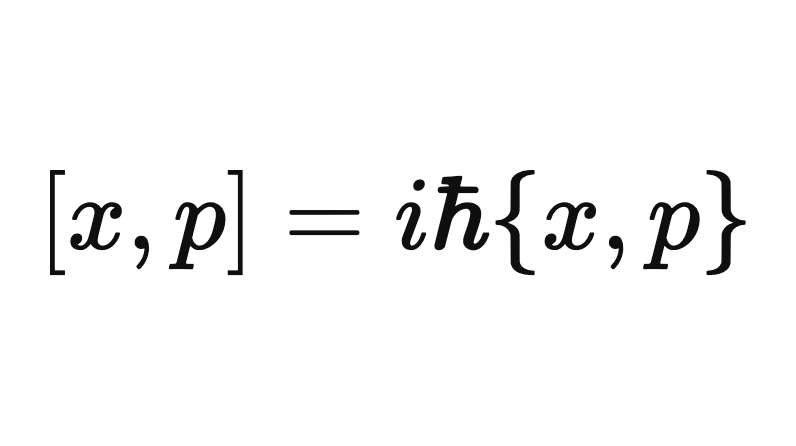
One thing that puzzled me while learning QM is the relation between the quantum mechanical commutator and the Poisson bracket from classical mechanics. In part surely because i knew nothing about hamiltonian mechanics at the time, but, even after getting comfortable with that, i was still confused for the connection.

It was until yesterday, that is. It finally clicked when reading (Dirac 2010): the algebraic properties of the Poisson bracket, together with the non-commutativity of QM observables, basically fix the relation between the commutator and the Poisson braket.

The Poisson bracket in Hamiltonian mechanics.

In hamiltonian mechanics, one uses the positions $x^i$ and momenta $p_i$ of the system, which together determine the phase space of the system, and a special function $H$, the hamiltonian of the system, ie the energy. Then one has the hamilton equations:

${\displaystyle \frac{\mathrm{d}{x}^i}{\mathrm{d}t}=\frac{\mathrm{\partial }H}{\mathrm{\partial }{p}_i}\frac{\mathrm{d}{p}_i}{\mathrm{d}t}=-\frac{\mathrm{\partial }H}{\mathrm{\partial }{x}^i},}$

which determine the time evolution of the system.

One can write the hamilton equations by defining the Poisson bracket ${,}-$a thing that takes two functions on phase space, and spits out another function, as follows:

${\displaystyle \{f,g\}=\sum _i(\frac{\mathrm{\partial }f}{\mathrm{\partial }{x}^i}\frac{\mathrm{\partial }g}{\mathrm{\partial }{p}_i}-\frac{\mathrm{\partial }f}{\mathrm{\partial }{p}_i}\frac{\mathrm{\partial }g}{\mathrm{\partial }{x}^i})\mathrm{.}}$

The equations now are

${\displaystyle \frac{\mathrm{d}{x}^i}{\mathrm{d}t}=\{x^i,H\}\frac{\mathrm{d}{p}_i}{\mathrm{d}t}=\{p_i,H\}\mathrm{.}}$

Now the equations are slightly more symmetric, big deal. But actually, we can express the time evolution of any function of position and momenta in the same way! Indeed, let $f=f(x,p)$, then

${\displaystyle \begin{array}{rl}{\displaystyle \{f,H\}}& {\displaystyle =\sum _i(\frac{\mathrm{\partial }f}{\mathrm{\partial }{x}^i}\frac{\mathrm{\partial }H}{\mathrm{\partial }{p}_i}-\frac{\mathrm{\partial }f}{\mathrm{\partial }{p}_i}\frac{\mathrm{\partial }H}{\mathrm{\partial }{x}^i})}\\ {\displaystyle }& {\displaystyle =\sum _i(\frac{\mathrm{\partial }f}{\mathrm{\partial }{x}^i}\frac{\mathrm{d}{x}^i}{\mathrm{d}t}+\frac{\mathrm{\partial }f}{\mathrm{\partial }{p}_i}\frac{\mathrm{d}{x}^i}{\mathrm{d}t})}\\ {\displaystyle \{f,H\}}& {\displaystyle =\frac{\mathrm{d}f}{\mathrm{d}t}\mathrm{.}}\end{array}}$

Neat! The hamiltonian, via the Poisson bracket, determines the time-evolution of any function on phase space; the hamilton equations for $p$ and $x$ are just a special case.

The commutator in QM

A lot of people learn QM in the Schrödinger picture, in which the state of the system evolves, and the operators stay put. But for many uses, its more practical to use the heisenberg picture$-$in which the observables evolve and the state stays put. The equations of motion in the heisenberg picture are then:

${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}O=\frac{i}{\mathrm{\hslash }}[O,H],}$

where $O$ is some observable, $H$ is the hamiltonian, and

${\displaystyle [O,H]=OH-HO\mathrm{.}}$

If we want for the observables in QM to follow the same equations of motion as in classical mechanics, we clearly need to have the relation

${\displaystyle [O,H]=i\mathrm{\hslash }\{O,H\},}$

the classic example being

${\displaystyle [x_i,p^j]=i\mathrm{\hslash }{\delta }_{ij}\{x_i,p^j\}={\delta }_{ij}\mathrm{.}}$

One could stop here, but I always found it weird that the commutator, a fundamentally algebraic notion, could be related in such a direct way with the the Poisson bracket, something that has such a calculus vibe.

It had to be this way.

In fact, the algebraic properties of the Poisson bracket and the non-commutativity of the QM observables fix their relationship.

Note that the Poisson bracket satisfies the Leibniz rule (aka the product rule):

${\displaystyle \{f,g{g}^{\mathrm{\prime }}\}=g\{f,g^{\mathrm{\prime }}\}+\{f,g\}{g}^{\mathrm{\prime }},}$

and similarly for ${ff',g}$ This is a direct consequence of the definition, but also it had to be this way since to be consistent with the hamilton equation $(gg')/ t={gg',H}$. Note that for commuting quantities, it does not matter if we write the right hand side as above or as ${f,g'}g+{f,g}g'$, but for non-commuting observables, we preserve the ordering.

It turns out this pretty much fixes the relation between the commutator and the poisson bracket!

Let’s see Consider the bracket ${ff',gg'}$. We can expand the right side first, and then the left:

${\displaystyle \{f{f}^{\mathrm{\prime }},g{g}^{\mathrm{\prime }}\}=g\{f{f}^{\mathrm{\prime }},g^{\mathrm{\prime }}\}+\{f{f}^{\mathrm{\prime }},g\}{g}^{\mathrm{\prime }}=gf\{f^{\mathrm{\prime }},g^{\mathrm{\prime }}\}+g\{f,g^{\mathrm{\prime }}\}{f}^{\mathrm{\prime }}+f\{f^{\mathrm{\prime }},g\}{g}^{\mathrm{\prime }}+\{f,g\}{f}^{\mathrm{\prime }}{g}^{\mathrm{\prime }}}$

or in the other order

${\displaystyle \{f{f}^{\mathrm{\prime }},g{g}^{\mathrm{\prime }}\}=f\{f^{\mathrm{\prime }},g{g}^{\mathrm{\prime }}\}+\{f,g{g}^{\mathrm{\prime }}\}{f}^{\mathrm{\prime }}=fg\{f^{\mathrm{\prime }},g^{\mathrm{\prime }}\}+f\{f^{\mathrm{\prime }},g\}{g}^{\mathrm{\prime }}+g\{f,g^{\mathrm{\prime }}\}{f}^{\mathrm{\prime }}+\{f,g\}{g}^{\mathrm{\prime }}{f}^{\mathrm{\prime }},}$

and these two expressions need to be the same. Equating them, and rearranging some terms:

${\displaystyle [f,g]\{f^{\mathrm{\prime }},g^{\mathrm{\prime }}\}=\{f,g\}[f^{\mathrm{\prime }},g^{\mathrm{\prime }}]\mathrm{.}}$

Now, this expression must hold regardless of the choices of the specific functions. One way to ensure this is to have

${\displaystyle [f,g]\propto \{f,g\}\mathrm{.}}$

If we had to this the requirement that the poisson bracket of two self-adjoint operators to be self adjoint (to be compatible with the hamilton equation), we should impose

${\displaystyle [f,g]=iC\{f,g\},}$

for some real constant $C$. Then $C=$ is fixed by experience.

And there you have it: the poisson bracket for non-commuting observables has to be related to their commutator!

Caveats

This is in no way a derivation, but a post-hoc justification/motivation for the heisenberg equation of motion. We glossed over (ie ignored) loads of subtleties. Also, there is a lot of beautiful geometry flowing from the Poisson bracket, which i hope to write about some day.

---

Bibliography

---

---

---

---